QUANTUM CHEMISTRY
Quantum chem
H and E where H is Hamiltonian constant and E is energy in joules.
H ψ = E ψ , where ψ is the wave function governing the probability that describes of position of electron.
Hx = Hamiltonian for one dimension trajectory along x axis is given by the expression [- ℏ/2m] ∂2ψ/∂x2 + PEx
[- ℏ/2m] ∂2ψ/∂x2= KINETIC ENERGY along x axis
PEx =Potential energy at position x
De-Brogli wavelength λ =h/p
h=Planck’s constant = 6.6256 x 10-34 Js
ℏ = h/2π
p = linear momentum in given direction or axis
Kinetic energy (1/2)mv2 = p2/2m
where m is the mass or reduced mass and p is momentum and v is velocity ( v = p/m )
Therefore, one dimensional time independent radial form of Schrodinger expression for the total energy in x-axis of a particle with trajectory wavefunction ψ is
[-ℏ/2m] ∂2ψ/∂x2 + PEx = Eψ
(Amplitude of a wave )2 = intensity of wave particles causing the wave motion
(Amplitude of a light wave )2 = intensity of light = probability of photon presence.
ψ2 = ψ* x ψ = probable presence of the wave particles (photon).
For a region of space between y and y+dy, probable location of particle = ψ2 ∂y
Wavefunction ψ has positive regions and negative regions, but ψ 2 is always positive and real.
ψ 2 = probability density
VOLUME SITUATION:
In a 3-dimensional volume situation, (region of axis x,y and z)
Probability =ψ 2 dv where or V =[X][Y][Z] , dv= dxdydz
QUESTION:
For a 1-dimensional wavefunction,ψ=e -b/3 find the relative probability for particle presence at b = 0 and b =3 in a region of length = 5pm from the center. [b = xo/1pm].
Answer:
Approximate probability = P (approx ) =ψ 2 dy for b=0 , e-0 = 1 . , thereforeψ 2 dy =12 dy where dy = 5pm ,
Therefore P (approx) = 12(5pm).
For the location b =3 ;
ψ 2 = (e -b/3 )2 = e-2b/3 , therefore if b=3 then ψ2 = e-2 = 0.135(5pm) = P (approx)
Relative probability = P approx b=0 / P approx b=3 = 12(5pm)/ 0.135(5pm) = 7.407
NORMALIZATION:
N2 ∫ψ ψ =1
Using a constant to find solutions of wave-function equations ; where N = Constant and real
Therefore, probability density becomes (Nψ )2
Probability in a small region (x=dx ) becomes Nψ 2 dx
All probabilities in a region dx add up to 1.Nψ 2x=(1-∞) dx (1-∞) = 1
∫(Nψ) 2 dx = 1 , or ψ 2 = ψ*ψ where ψ* is a complex variable of ψ
Therefore, normalization can also be written as N x N ∫ ψ * ψ dx = 1
N 2 ∫ (ψ 2 ) dx = 1
N = 1/ [ ∫ (ψ 2 ) dx] ½
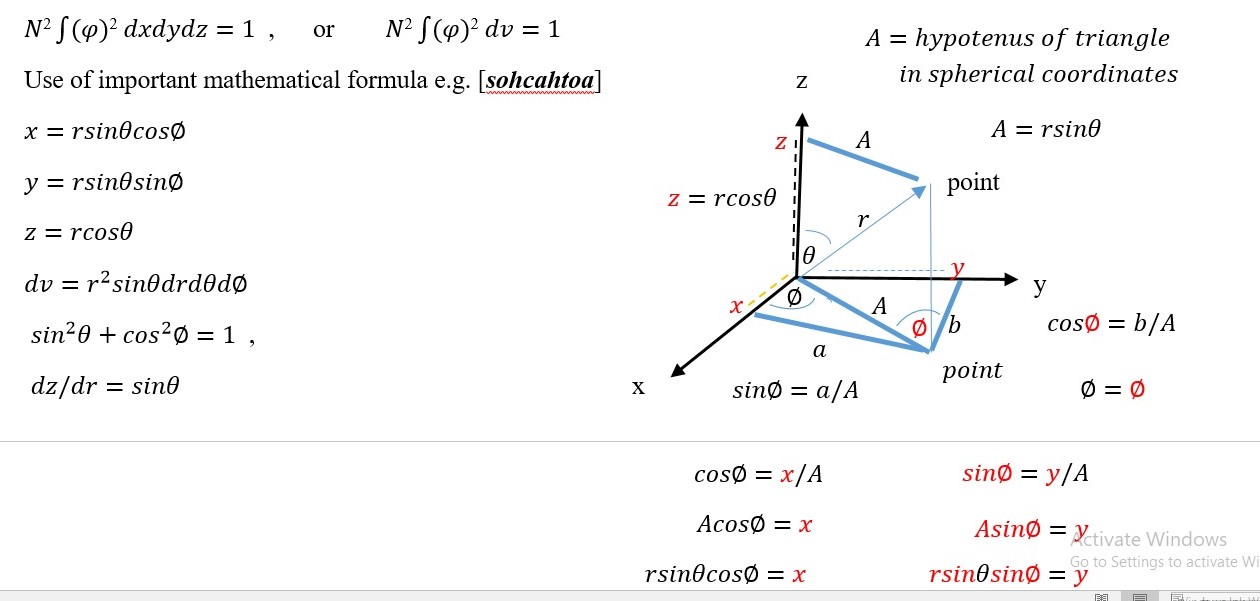
Using the above formula gives;
N2 ∫ (ψ 2 ) dxdydz =1 or N2 ∫ (ψ 2 ) dv = 1

N2 ∫0∞ (ψ 2 ) dv = 1
The range of integrals that is chosen is important for the solutions of equations involving the wave function to be continuous, with continuous slope , one value (energy of particle is quantized) , and finite everywhere ( real value).
If only kinetic energy (K.E.) exist for particle in motion, then total energy = E = K.E.= H (Hamiltonian)
Then Eψ = (K.E.) ψ = – ℏ/2m] ∂2ψ/∂x2 where ψ= Aeikx + De-ikx where A and D are constants.
What is Hamiltonian operator refers to ;
Observable property = property that can be measured or quantified or quantized e.g. speed or momentum or intensity of a wave or particle.
Operator = the formula that gives the solution or value of the observable property (e.g. value of energy, momentum or velocity).
Example and energy in x dimension of a wave particle in motion, H = KE (x)+ PE (x) .
H = [- ℏ/2m] ∂2/∂x2 + PE(x)
The higher the value of ∂2/∂x2 , the larger the wave curvature = steep slope or shape = larger kinetic energy = smaller wavelength(λ) = smaller potential energy along the axis. This applies to all waves or wave functions.
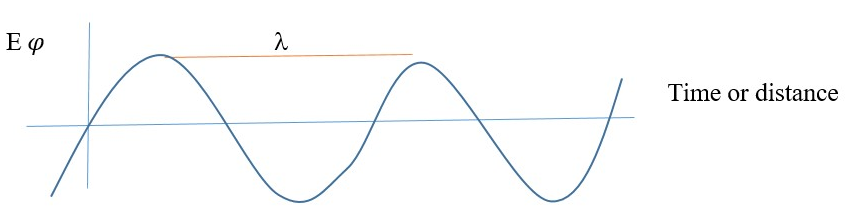
Broad curvature = smaller value of slope of wave
Large PE or Small KE
Large wavelength (λ) , lower frequency.
On the other hand, short wavelength gives the opposite description,

Sharp curvature = steep or large slope of each slope of wave
Small or decreased PE, Large KE or increased KE
Smaller wavelength (l) , higher frequency.
Example given below.

Operator [wave function] = Value [wave function]
In very simple terms.
When one calculates the speed of an object or particle, the property of the particle [formula set up] that enables calculation of the speed is the Operator and the calculated answer for the speed is the Value and the unit of the value is the wave-function. e.g.
[Distance/time]m/s = 5m/s
[mass x acceleration] newtons = [Force] newtons
[Work]joules = [energy] joules
[Force x distance] joules = [energy]joules
[Force x distance] kgm/s2 = [value] kgm/s2
[operator]function property = [ expectation value] function property
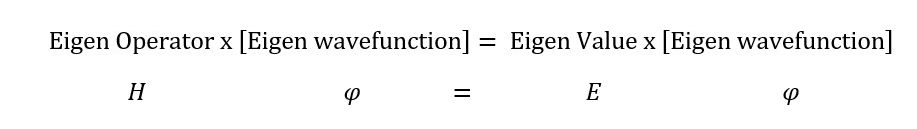
Questions and Answers:


Questions and Answers ;
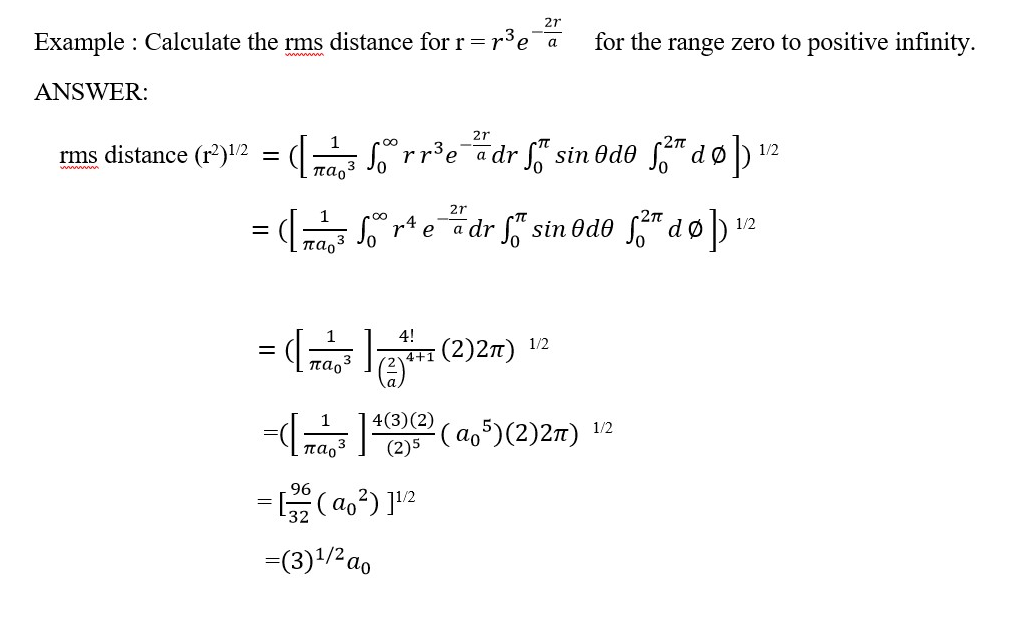
The Uncertainty Principle:
Uncertainty in the value of position and momentum of an object cannot be both equal to zero at the same time along the same point of reference axis.
Δx Δpx ≥ ℏ/2 ,
px = momentum in x-dimension,
Δx = uncertainty in position of particle in x-dimension
Δ px= uncertainty in x-dimension momentum of particle,
ℏ = h/2p
Δx Δpx ≥ h/4p
v = p/m or p=mv
Δx Δvx ≥ ℏ/2m or Δx Δvx ≥ h/4pm or Δx Δvx ≥ h/4pm
where vx = velocity in x-dimension .
m =mass of particle causing the wave.
Δvx = uncertainty in velocity in x-dimension
Δx = 0 implies no uncertainty in position of the particle causing the wave = exact position of particle is known.
Implies Δpx or Δvx is infinity = speed or velocity cannot be known in the x-dimension.
Infinite number of different wave functions add up to cancel out due to positive and negative parts but point of same sign will add to form a sharp single peak to indicate high probability of locating particle at this position. However, it will be very difficult to identify the exact single momentum causing that peak at this position since it is made of infinite number of waves of different amplitudes and momentum.

If Δvx = 0 no uncertainty in speed or velocity in x-dimension.
Implies speed or velocity or momentum in x-dimension is exactly known.
(This means Δx = infinity; uncertainty in position in x-dimension is infinite = exact position of particle cannot be known in x-dimension).
Time and distance travelled can be measured to find the exact velocity and momentum, but exact position of particle is unknown.
Order of different quantum observables around an operator do not interchange because they are complementary and do not commute to the same result (e.g. position and momentum)]. Different observables have different probabilities so the operator can only measure one observable property at a time and not more than one. [uncertainty principle].
A [OPT] B ≠ B [OPT] A
Observable A Operator observable B
Common examples of usage of quantum chemistry:
Particle in the Box :
This is a situation in which a particle with some definite momentum is confined to a specific region of space. Kinetic energy is maximum within the boundaries, but potential energy is zero. Kinetic energy of particle at the boundary is zero but potential energy is infinite at the boundaries.
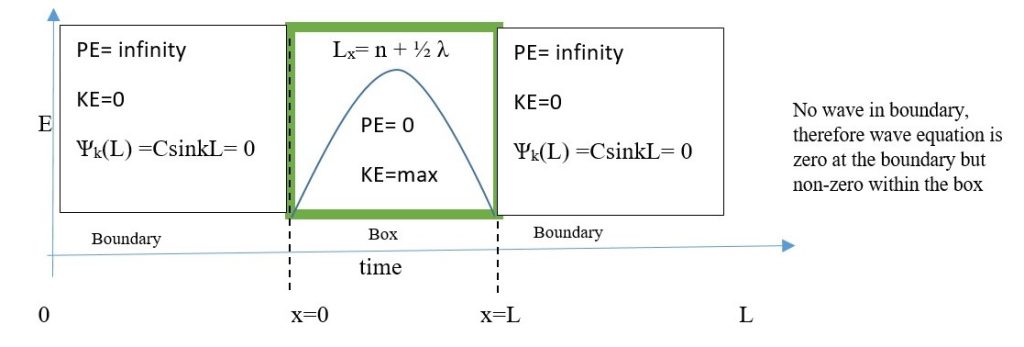
Conditions:
K.E. is maximum within the boundaries, where P.E. is zero.
PE is infinite at or within the boundary walls, KE is zero at or within the boundary walls.
The sine wave shown is described by the equation ; Ѱk(L) =CsinkL
where C is a constant, kL=nπ and n=positive whole number.
therefore k= nπ/L
Ѱn(x) =Csinkx where x is a specific value along L. , therefore this gives ;
Ѱn(x) =Csin nπx/L
E = [- ℏ/2m] ∂2ψ/∂x2 the solutions will give energy;
E=k2ℏ2/2m
substitute k= nπ/L will give
E= n2π2ℏ2/(2mL2 ) ,
substituting ℏ = h/2π will give
E= n2π2h2/(2mL2 4π2)
= n2h2/(8mL2)
You can also use De-Brogli wavelength and boundary conditions to get the same answer;
L= n + ½ λ , momentum p = ℏ/ λ = n ℏ/2L
and quantized energy En= p2/2m
ѰkE(y) =Csink(y) + Dcosk(y)
implies at y=0, ѰkE(y) = D
Ѱ(0)(0) =0 ,
ѰkE(y) =0 implies, D=0 at y=0
ѰkE(y) = Csink(y) at y=L
ѰkE(y) = Csink(y)
= CsinkL =0
Therefore, C= 0 is a violation of Born interpretation because it implies the particle is not present, therefore keep C but work on sinkL. Same results for one dimensional motion in x and z axis.
kL=n π
n≠ 0 , n=1,2,3…
E α n2 , relative energies allowed for n values of the particle in the box E = n2h2/(8mL2)

DEGENERACY OF WAVEFUNCTIONS
Energy equations for wave functions give same results for different values of n
if L1=L2=L3 etc.
Ѱn=1,n=2,n=3(x,y,z) = (2/L) [sin(n1π x/L1) sin(n2 π y/L2) sin(n3 π z /L3) ]
E = n12 + n22 + n32 [h2/(8mL3)]
For a 3-dimensional cube, L=L1=L2=L3 and nx, ny and nz values will always commute to give the same result for energy value.
E.g.
Ѱnx=1,ny=2,nz=1(x,y,z) = (2/L) [sin(π x/L1) sin(2 π y/L2) sin( π z /L3) ] ,
E = [- ℏ/2m] ∂2ψ/∂x2 the solutions give
E = (12 + 22 + 12 ) [h2/(8mL3)] = (¾)[h2/(mL3)]
We will get the same results for nx=1, ny=1 and nz=2 .
This implies wave functions; Ѱn1,,n2,n3(x,y,z) , Ѱn2,,n1,n3(x,y,z) , Ѱn3,,n1,n2(x,y,z) are equal in energy and therefore gives DEGENERATE energy states. This is related to the symmetry of the system e.g. square or cube and not a rectangle. Square or cube has all equal sides or length thus rotation on either side is the same. A rectangular system will not give degenerate energy states.
TUNNELING
Total energy of wave particle, E total = kinetic energy + Potential energy = K.E + P.E
At max K.E of wave particle propagation, P.E wave particle propagation = 0,
Therefore, E total = K.E.
At energy barrier wall, K.E = 0, P.E = infinity.
This means, E total of wave particle = P.E. of particle at wall barrier
This means particle is infinitely trapped in position.
Particle cannot cross the barrier and go outside barrier.
However, in real situations, the particle can go through the energy barrier and come outside at the opposite end and still propagate as a wave. This is called TUNNELING.
This occurs because in real situations the barrier P.E is finite not infinite;
Therefore, finite P.E of barrier > E total of particle.
This means even though, the total energy of particle in wave is less than potential energy of barrier, the barrier imparts or allows some residual kinetic energy for particle to still move through barrier.
K.E. residual = P.E. barrier – E total (of moving particle in wave) .
K.E residual is positive energy.
This can occur when;
- Wall or barrier is thin such as air or vacuum.
- Wave particles are very light or small.
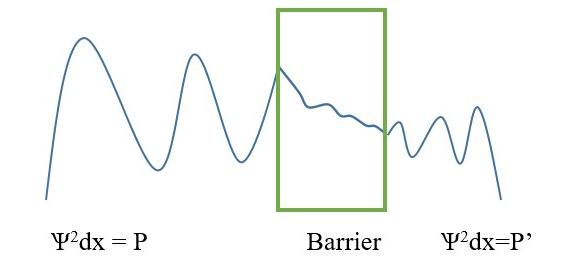
Wave propagation energy decreases exponentially as wave particle moves through barrier or wall and tunnels to reach outside to form continuous wave.
For every wave there are points of reflection back from right to left at incident point, but we are mostly concerned with the process of wave transmission through the barrier from left side of barrier to the opposite right-side end.
Tunneling transmission probability T = P’/ P
Tunneling, T = 16 ε (1- ε) e-2KL , Where ε = E total energy of wave particle / P.E barrier wall
Generally, ℏ2k2=2Me
In Classical physics, E total = P.E. at barrier wall
ε = E total / P.Ewall =1 , therefore T= 0.
However, in Quantum physics; tunneling will occur, for E total < P.E.
K= (2m x [ P.E. –Etotal ]/ ℏ2) 0.5
ε =E total of wave particle / P.E. wall is a very small value.
T > 0
Example of tunneling;
- Passage of electric current through a vacuum, insulator or non-polar medium (e.g. Scan Tunneling Microscopy STM).
- Chemical reactions with very high activation energy barrier and how catalyst or other means are employed for the reactions to occur despite the high energy barrier.
Tunneling can also be achieved by using wave particles with very high energy to overcome the potential energy of the barrier.
E total > P.E (of barrier),
Therefore,
Etotal – P.E. = + K.E. of wave particles;
+K.E. = > PARTICLE can tunnel across barrier.
ε = E total of wave particle / P.E (of barrier) = very large value.
T > 1


