ACIDS , BASES , SALTS , BUFFER SOLUTIONS, pH and pI

Salts, Acids , Bases and Buffers and pH

There are several ways to define an acid ,base or salt . One definition is Bronsted acid defines an acid as a proton donor). However, the Lewis acid definition makes an acid an electron pair acceptor. On the other hand , a base is a proton acceptor (Bronsted) or electron pair donor (Lewis definition). Salt is usually formed when an acid reacts with a base and one of the hydrogens is replaced by a metal atom. Bronsted acids contain hydrogen ions that can reacts in proton transfer reactions. Examples include of Bronsted acids include HCl, H₂SO₄ , HCIO₄, H₃PO₄  .

Lewis acids do not necessarily have to contain any hydrogen ions and examples are AlCl₃, FeCl₃ and BF₃.

Bronsted bases usually contain hydroxyl group (OH) and examples include NaOH , KOH, Mg(OH)_2. However, a Lewis base will be any species with electron pair that can be donated to react to form a bond. Examples include Sodium hydride (NaH)  , Ammonia (NH₃) , all the alkali and alkaline earth metals and their oxo-compounds. For example, sodium metal (Na) , Sodium oxide (Na₂O), Magnesium metal Mg, and Magnesium oxide (MgO) . Transition metals and their oxo-compounds can also be classified as Lewis bases.

All Bronsted bases can also function as Lewis bases vice versa. However, not all Lewis acids function as Bronsted acids. Sodium hydroxide can react with HCl to form sodium chloride (NaCl) salt and water.

A Buffer is a weak base with the salt of its conjugate acid or a weak acid with a salt of its conjugate base.

pH is a measure of hydrogen ion concentration. pH=-Log [H⁺]. Smaller pH value is more acidic but larger value is more basic. pH 7 is neutral.

Strong acid dissociates completely HA ^_________> H⁺ + A⁺

pH is –log [H+]

Strong bases dissociate completely

 e.g. NaOH ^_________> Na⁺ + OH^–

pOH= – log[OH^–]

pH + pOH = 14

pH=14- pOH

WEAK ACIDS

Do not dissociate completely in solution. Equilibrium is reached between ions and solid salt or molecules.

HA < = > H⁺ + A^–

k = Acid dissociation constant = Product concentration / reactants concentration = [H⁺][A^–] /[HA]rem

At equilibrium the HA produces equal H⁺ and A- , [H⁺] = [A^–]

Amount of initial acid remaining at equilibrium = [HA]rem = [HA] – [H⁺] ,

Sometimes, this is approximately equal to [HA] because of small dissociation. To avoid using quadratic equation.

Therefore, K = [H⁺]²/[HA]_rem     , or sometimes just, k = [H⁺]²/[HA]……1

Standard values of k for weak acids are calculated and known.

From eqn 1,   [H+] = (k[HA]rem)^1/2

PH = – Log [H+] = -Log [(k[HA]rem)^1/2] = -[½] ([ logk ]+ log[HA]rem])

PH = ½ (-logk –log[HA]rem)

=1/2 (pk- log[HA]rem)

Weak bases (B)

B  + HOH < = > BH + OH-

Base dissociation constant kb = [products] / [reactants] = ([ OH^–][ BH])/([ HOH ][B]rem) ; water is large excess solvent and ionization is taken as negligible compared to the base so ignore water

Kb = ([OH^–][ BH])/([B])

At equilibrium, Base forms [OH-] = [BH] ,    [B]_rem= [B]_o –[OH^–]

kb= ([OH^–]²)/([B]rem)

([OH^–]= (k_b[B]rem)^1/2

pOH=- log[OH^–] = -log (k_b[B]rem)^1/2)

=1/2(-logk_b – log[B]rem)

=1/2 (pk_b – log[B]_rem)

From ionic product of water, HOH < = > H⁺ + OH^– 

                                                                 10^-7   10^-7

[H][OH-]=10^-14= Kw =k x k_b

pkw = pk + pk_b

SALT SOLUTIONS

Salts of strong acids and bases dissociate completely in solution. The ions are hydrated and exist as neutral species and do not undergo any further interactions with water molecules to any extent as generate more protons or hydroxyl ions in solution.

NaCl    ^_______>    Na⁺     +       Cl^–  ………neutral

Salts of weak acids and bases do not dissociate completely and can form acidic or basic solutions

Acid salt = Salt of strong acid and weak base = forms acidic solutions

NH₄Cl     ^______>              NH₄⁺                     +                      Cl ^–

                       Weak conjugate acid                              neutral

NH₄⁺ + HOH   < = >       NH₃               +                     H₃O⁺              

                                    Weak base                             strong acid

k = [NH₃][H₃O⁺]/ [NH₄⁺]

Basic salt   =   salt of strong base and weak acid = forms basic solutions

NaOOCCH₂CH₃    ^________>   Na⁺     +        ^–OOCCH₂CH₃

                                          Neutral              weak conjugate base

HOH    +   ^–OOCCH₂CH₃   ^_________> HOOCCH₂CH₃           +             OH^–   

                                                          Weak acid                             strong base             

k_b = [HOOCCH₂CH₃ ][ OH^–] / [ ^–OOCCH₂CH₃ ]

BUFFER SOLUTIONS

Acid buffer:  Weak Acid + its salt of strong base   or   Weak acid and its salt.                                         

 E.g. HOOCCH₂CH₃   +   NaOOCCH₂CH₃

k = [H⁺][ NaOOCCH₂CH₃] / [HOOCCH₂CH₃]

[H⁺] = k[HOOCCH₂CH₃] / [NaOOCCH₂CH₃]

Basic buffer:  Weak base + its salt of strong acid   or    Weak base and its salt.                             

E.g.CH₃NH₂  +  CH₃NH₃⁺Cl

k_b = [OH][ CH₃NH₃⁺Cl] / [CH₃NH₂]

[^–OH] = k_b[CH₃NH₂] / [CH₃NH₃⁺Cl]

Principle of electroneutrality and quantitative analysis

Concentration of positive and negative charges must balance out to achieve electro-neutrality in a system.

Calculate the pH of a solution of a solution containing 0.03 mol of CaF₂ in 1.0 L water.

Answer:

CaF₂ is sparingly or partially soluble in water.

CaF₂  (aq) < = > Ca²⁺ (aq) + 2F^–   (aq)        Ksp = 4.0 x 10^-11  

                            s            +   2s   

where s=solubility of CaF₂ = concentration of Ca²⁺ ions,  2s = concentration of F- ions

[Ca²⁺ ] [F^–]² = Ksp = 4.0 x 10^-11  

[s] [2s]²= Ksp = 4.0 x 10^-11  

4s³ = Ksp = 4.0 x 10^-11  

s= [(4.0 x 10^-11   )/4 ]^1/3    =  0.0002154435M = solubility of 1mol CaF₂ in 1L solution , 0.03 mol CaF₂ will be [0.03mol / 1mol ] x 0.0002154435M = 0.0000064633 M

Therefore [Ca²⁺ ]= 0.0000064633 M   ,  [F^–]= 2 x 0.0000064633 M   = 0.0000129266 M

F- ion undergoes basic hydrolysis;

F^– + H₂O < = > HF + OH^–  Kb = ?

We know HF(aq) < = > H⁺ + F^–    Ka = 6.8 x 10^-4

Therefore Kw=k_bk_a   ,

kb = Kw/ka = (1.0 x10^-14 ) / (6.8 x 10^-4) = 1.471 x 10^{-11   …..} F^– + H₂O < = > HF + OH^– 

Kb= [HF][OH^–]/ [F^–] 

Concentrations are very low that we have to take into account self-dissociation of water  

H₂O  < = >  H⁺ + OH^–   [The OH^– from water will add to the OH^– from F^– hydrolysis]

[X][X+10^-7]/[ 0.0000129266-X]  = 1.471 x 10^-11  ,

We cannot approximate because of very low concentrations

[X][X+10^-7]  = [1.471 x 10^-11  ][ 0.0000129266-X]

[X][X+10^-7]  = [1.471 x 10^-11  ][ 0.0000129266-X]

X²+10X=1.9015×10^-16-1.471 x 10^-11  X

X² +10x +1.471 x 10^-11  X -1.9015×10^-16 = 0

X² +1.0015×10^-7 X -1.9015×10^-16 = 0

quadratic equation solution ;

X = (-1.0015×10^-7 +/- [( 1.0015×10^-7)²   +4(1)( 1.9015×10^-16  )] ^½ )/2(1)

   = 1.86639 x 10^-9 M

Therefore [HF]= 1.86639 x 10^-9 M

[OH^–] = 1.86639 x 10^-9 M +10^-7M=1.01866 x10^-7M

[F^–]  = 0.0000129266 – x = 0.0000129266M -1.86639 x 10^-9 M = 0.0000129247M

pOH=-log [1.01866 x10^-7] = 6.9919691    pH=14 – 6.9919691 = 7.008130933,  [H⁺]=9.816 x 10^-8M

Charge balance:   [H⁺] + 2[Ca²⁺] = [OH^–] + [OH^–] + [F^–]

Mass balance:     [HF] +  [H⁺] + 2[Ca²⁺] = [OH^–]+  [OH^–] + [F^–]

 1.86639 x 10^-9 M + 9.816 x 10^-8M + 0.0000129266 M = [1.01866 x10^-7M+ 0.0000129247M]

                               1.30266 x 10^-5 M                              =                 1.30266 x 10^-5 M  

This proves that mass balance is correct.

The solution is almost neutral due to low concentration of the insoluble salt CaF_{2  .}

P.S. Try and calculate the pH of 0.03mol KF in 1.0L water and compare result withCaF₂  explain the difference between the results.

Question Example:

0.0350mol KH₂PO₄ was added to 0.040mol KOH in 1L water.

Calculate the concentration of each species in solution and the pH of the solution.

ANSWER:

Charges or ions in the solution:

 KH₂PO₄    Consist of K⁺ +  H₂PO₄ ^–  

KOH ^________> K ⁺ + OH^–    

Mole ratio ; mol K+ / mol OH- = 1/1 , this implies 1mol K+ = 1mol OH-

[K⁺] = [OH^–] for a solution of KOH only.

However, reaction between OH- ions and hydro-phosphate ion occur in solution to produce more ionization:

OH^–  +  H₂PO₄ ^{–      _____}>  HPO₄ ^-2     +      H₂O 

Extra OH remain reacts further to form more ions.

OH^–  + HPO₄ ^{-2     _______}>   PO₄ ^-3    +  H₂O 

All OH^– ions used up in this step. However, a typical complete hydrolysis reaction between water and the phosphate ions reforms some OH-ions ;

PO₄ ^-3    and some HPO₄ ^-2     reacts with water [reversible] = hydrolysis

HPO₄ ^-2      + H₂O < = > H₃PO₄^–   + 2OH^–

Therefore, the mole ratio =  mol OH^–/mol HPO₄ ^-2      = 2/1

1mol OH^– = 2mol HPO₄ ^{-2      ,}

this implies [OH^–] = 2[ HPO₄ ^-2  ] 

PO₄ ^-3    + H₂O < = > H₃PO₄        +  3OH^–

mol OH^–/ mol PO₄ ^-3    = 3/1

1mol OH^– = 3mol PO₄ ^-3    

this implies [ OH^–] = 3 [ PO₄ ^-3   ]

Charge balance: list any possible ion present in solution including dissociation of water:

[H⁺] + [K ⁺ ] = [OH^– ] + [H₂PO₄ ^– ] + 2[HPO₄ ^-2  ]+ 3[ PO₄ ^-3  ]. This is just listing all possible ions involved.

Mass balance:

This involves quantitative amounts of any species that contribute significantly to the concentration of the solution.

[K⁺]  = [OH^–] + [H₂PO₄ ^– ] + 2[HPO₄ ^-2]     +  3[PO₄ ^-3]  

Concentration or sum of the concentration of the positive charges should be equal to concentration or sum concentration of negative charges.

Calculations should prove this:

KOH is a strong electrolyte and dissociates completely to ions. Therefore, 0.04 mol KOH Contains 0.04mol K⁺ ions and 0.03mol OH^– ions.

KH₂PO₄  is a strong electrolyte and dissociate completely . Therefore, 0.035mol KH₂PO₄ contains 0.035mol K⁺ ions and 0.035mol H₂PO₄^–.

The OH- (0.03mol) base picks or reacts with protons in H₂PO₄^– (0.035mol) to form HPO₄^-2 , (0.035mol) and H₂O. Excess OH- (0.005mol) that remains converts some amount of HPO₄^-2 ions to PO₄^-3 ions

(0.005mol), leaving [0.035-0.005] mol or 0.030mol HPO₄^-2 ions.

After the complete dissociation, we have to calculate the amounts of each ion formed from each stage of the reversible incomplete basic hydrolysis reactions with water shown.

H₂PO₄^–                      +            H₂O     < = >   H₃PO₄    +   OH-     …….…… k_b =1.3 x 10^-12

0.0M [all reacted with OH^–]                             0.0M

Hydro phosphate ion hydrolysis

HPO₄^-2             +            H₂O   < = >   H₂PO₄^–        +     OH-      ………………. k_b =1.6 x 10^-7

[0.030-X] M                                          X                        X      (where X is equilibrium amounts formed)

k_b =1.6 x 10^-7 = [H₂PO₄^–][OH-]/[ HPO₄^-2]     

1.6 x 10^-7 = [X][X]/[ 0.030-X]   

 The value of k_b is very small, therefore approximate   0.030-X = 0.030M

Therefore, 1.6 x 10^-7 = [X][X]/[ 0.030]  , X = 6.928 x 10^-5M 

Therefore, this step forms

 [H₂PO₄^–]=[OH-]= 6.928 x 10^-5M    

[ HPO₄^-2] =   [0.020-X] =[0.030-6.928 x 10^-5 ]M   = 0.029930718M

Phosphate ion hydrolysis

PO₄^-3           +                   H₂O     < = >                  HPO₄^-2      +       OH-         . …… k_b = 2.1 x 10^-2

0.005-X                                                     0.029930718+ X               X

k_b = 2.1 x 10^-2 = [HPO₄^-2][OH- ]/[ PO₄^-3 ]

1. x 10^-2 = [0.029930718+X][X ]/[ 0.005-X ]

Value of k_b is huge so we cannot approximate so we have to work through;

X(0.029930718+X) = 0.021(0.005-X)

X²-0.050930718X-0.000105= 0

Use quadratic formula solution:

X = (-0.050930718 +/- [(0.050930718)² + 4(0.000105)]^0.5   ) / 2(1)

X = 0.001984313M

[HPO₄^-2]= 0.029930718+ X = [0.029930718+0.001984313]M= 0.031915031M

[OH- ]= 0.001984313M 

[ PO₄^-3 ] = [ 0.005-X ] = [ 0.005- 0.001984313]M=0.003015687M

Total Sum of ions listed;

All ions are contained in 1.0L volume so every mole of substance forms a concentration of Molarity M units.

[K⁺] = 0.04M + 0.035M = 0.075M

[OH^– ]= 0.001984313M   +  6.928 x 10^-5M     = 0.002054M

[H₂PO₄^–]= 6.928 x 10^-5M       

     [HPO₄^-2]= 0.031915031M

     [ PO₄^-3 ]= 0.003015687M

Check mass balance to see if our calculation is correct electro-neutrality of charges.

       [K⁺]    =       [OH^–]    +         [H₂PO₄ ^– ]      +          2[HPO₄ ^-2]             +            3[PO₄ ^-3]  

0.75M = (0.002054M) + (6.928 x 10^-5M ) + (2 x 0.031915031M)  + (3 x 0.003015687M)  

This proves we are correct.    

pOH =-log[OH^–] = -log (0.002054) = 2.69

pH = 14-2.69 = 11.31

[H⁺] = 10^-11.31    = 4.9 x 10^-12 M

AMINO ACIDS: pH AND pI

Living organisms contain proteins

Proteins consist of Amino acids: Amine group and Carboxylic acid group

AKA alpha-amino acid because amine group is on alpha carbon next to carboxylic group.

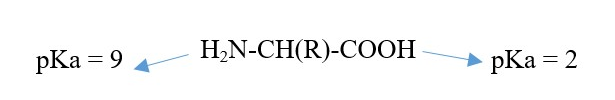
Ionization occur in solution of pH different from pKa of amino or acid group. The R group can affect the pKa if it is an amino or a carboxylic acid.

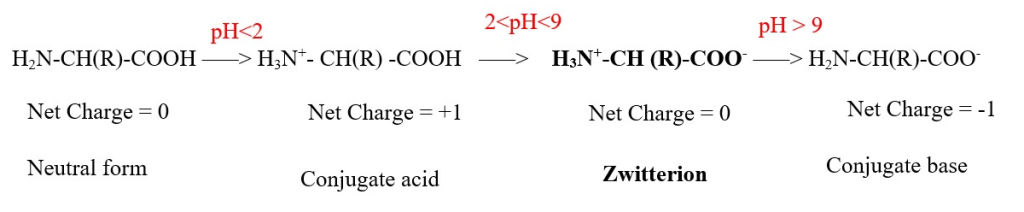
Zwitterion = equal number of positive and negative charges = total net charge = 0. This is Isoelectric form or Iso-ionic form. This is used to calculate the pI or isoelectric pH.

Isoelectric pH = pI = average mean value of pKa values of amino and acid groups excluding pKa of the main alpha COO- group of ZWITTERION.

Titration curve of a typical amino acid (AA) sample with different amounts of base.

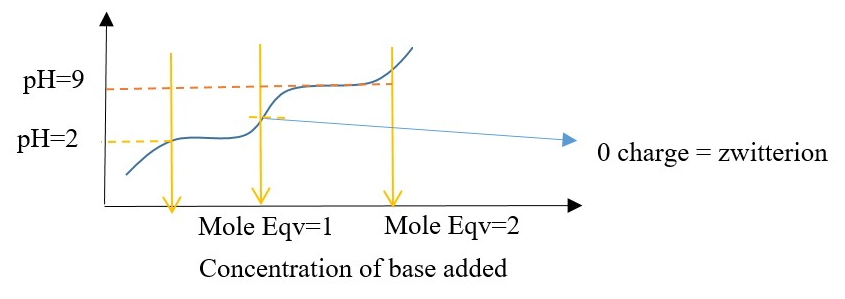
ELECTROPHORESIS:

Using electricity to separate amino acid or proteins.

pH< pI = positive form of AA= [will migrate to negative electrode when electricity is applied]

pH > pI = negative form of AA= [will migrate to positive electrode when electricity is applied]

pH = pI = net 0 charge =neutral or zwitterion form of AA= [ will not move when electricity is applied]

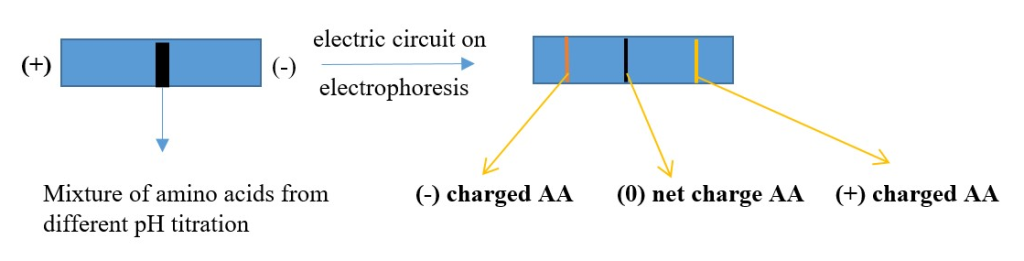
Several methods of electrophoresis exist

Example is Isoelectric focusing electrophoresis: charged proteins moving through electric field in a pH gradient support till pI of AA is reached then AA stops moving. Different proteins consist of different AA thus we get different travel distance of protein AA.

Question example :

  Calculate the pI of arginine and show the different forms of the amino acid at different pH values.

Answer;