SYMMETRY ELEMENTS AND POINT GROUPS
SYMMETRY ELEMENTS
The use of symmetry elements has enabled shape of objects to be classified in categories for identification. This however is used in chemistry to classify the shape of the structure of chemical compounds into different groups based on the symmetry elements that can be found in the structure of the compound. The elements include, E, Cn, I, Sn and σ.
IDENTITY ELEMENT (E)
This is the symmetry element obtained by viewing the shape of an object or the structure of compound when nothing is done to it. This implies doing nothing or viewing the structure of the compound through several angles or axis in space and arriving back at the same original position as if nothing has happened before. This is like turning an object through 360-degree angle. Every object has E symmetry element. 
AXIS OF ROTATION (Cn)
Cn is a symmetry element that refers to the axis or direction by which we can turn an object to obtain a view of the shape that cannot be differentiated from the first view. This can occur along multiple axis or viewpoint on the object. Each turn or rotation in a particular direction or plane is Cn axis is (Cn) where n is the maximum number of turns needed to obtain an indistinguishable view in the particular plane or direction. Turning the object to get an indistinguishable view is a Cn (n= number of turns by which the original shape can be obtained). A turn of one 180 degree to get an indistinguishable view is a C2 axis. If only one turn of 360 degrees can give the indistinguishable view, then we have a C1 or E.
Principal Cn axis is maximum number of turns needed to obtain indistinguishable view of the shape of an object.
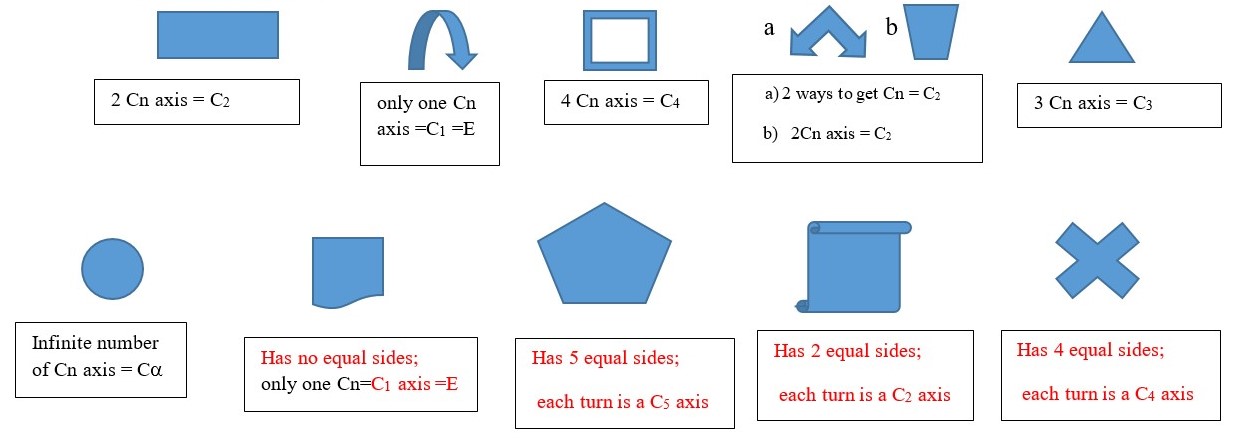
Subsidiary Cn axes:
Any Cn axis less than the principal Cn axis is a subsidiary axis. Some objects have other Cn axes in addition to the main principal Cn axes, for example a square has a C4 principal axes, but it also has four C2 axes. An equilateral triangle has C3 principal axes and three subsidiary C2 axes.
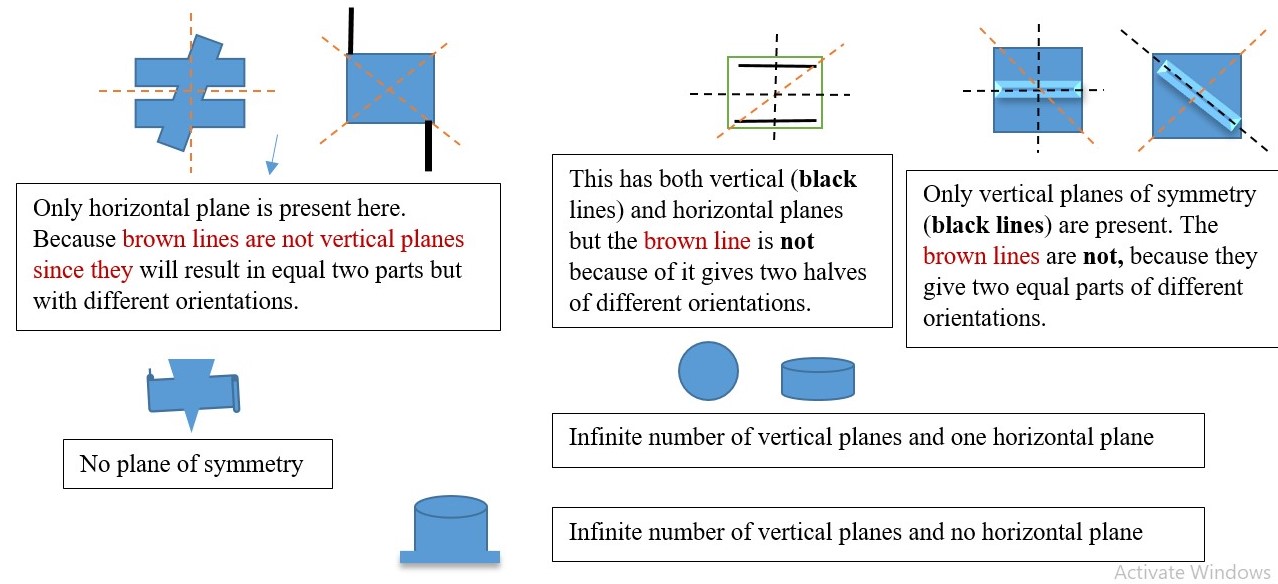
PLANE OF SYMMETRY ( σ )
σ is the symmetry element obtained by viewing the object along a plane that divides the object into two equal parts. This can be a vertical or horizontal plane.
Horizontal plane (σh) is the plane that cuts through along the plane of the page but is perpendicular to the principal axis.
A vertical plane (σv) cuts through the object out and above the shape into two equal parts but it contains or coincides with the principal axis.
The 2-d shape of some objects can have multiples vertical planes of symmetry (σv) but only one horizontal plane of symmetry (σh) if possible while other objects have no plane of symmetry.
σh (plane of the page)
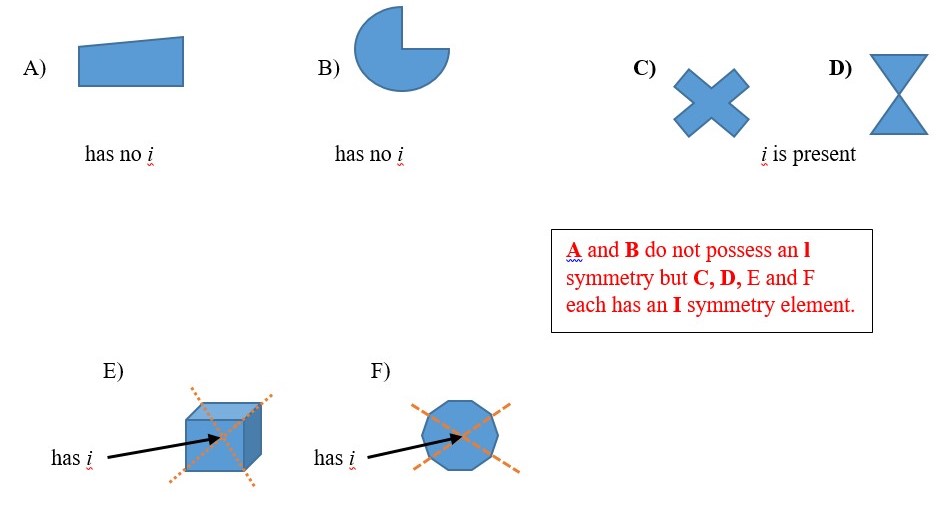
CENTER OF INVERSION (i )
I or center of inversion is a symmetry element that is present if all the point locations on one half of an object connects along lines that crosses the center to reach points of the same kind at the opposite half equal distance from the center. This cannot be really done on a real object or model structure. [Trying to look simultaneously the front and back of a ruler will end up breaking the ruler.]
IMPROPER ROTATION (Sn)
Sn is the symmetry element obtained by turning the object clockwise along a principal Cn axis and then viewing the object reflected image through a plane right-angled to the Cn axis. This is called improper rotation of the object.
Example of illustrations
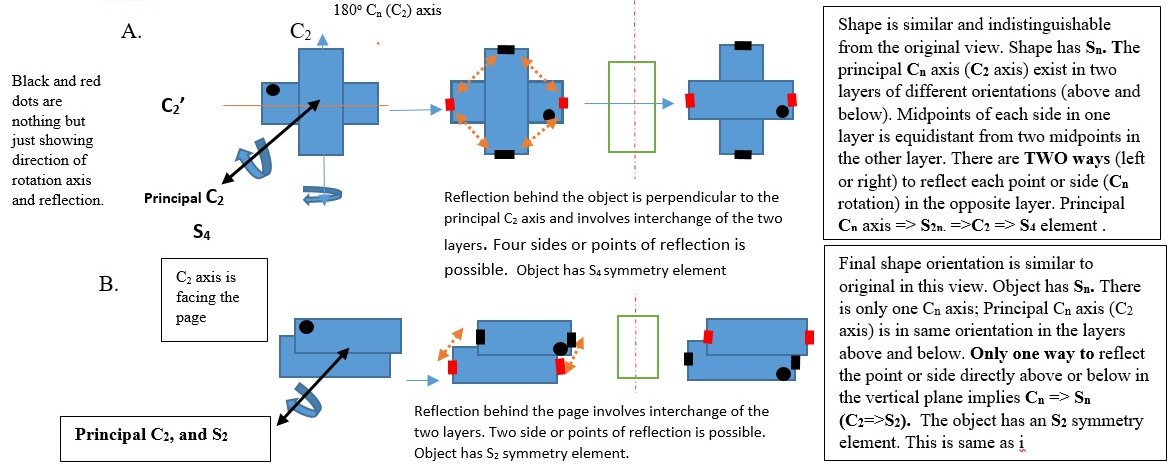
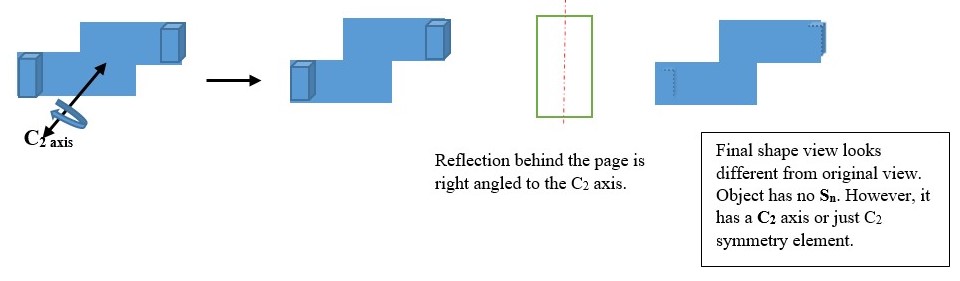
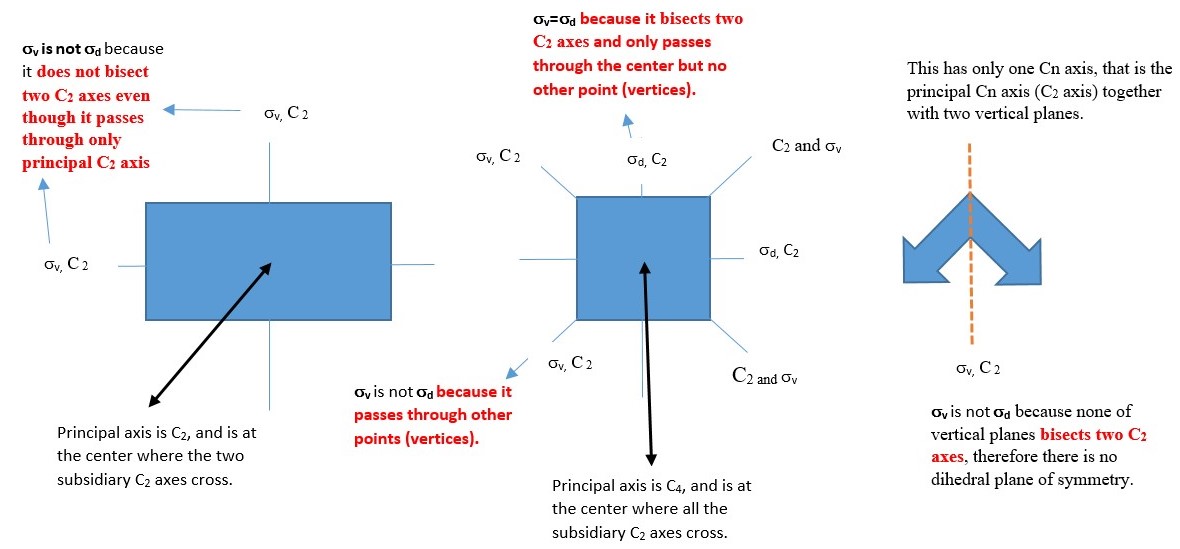
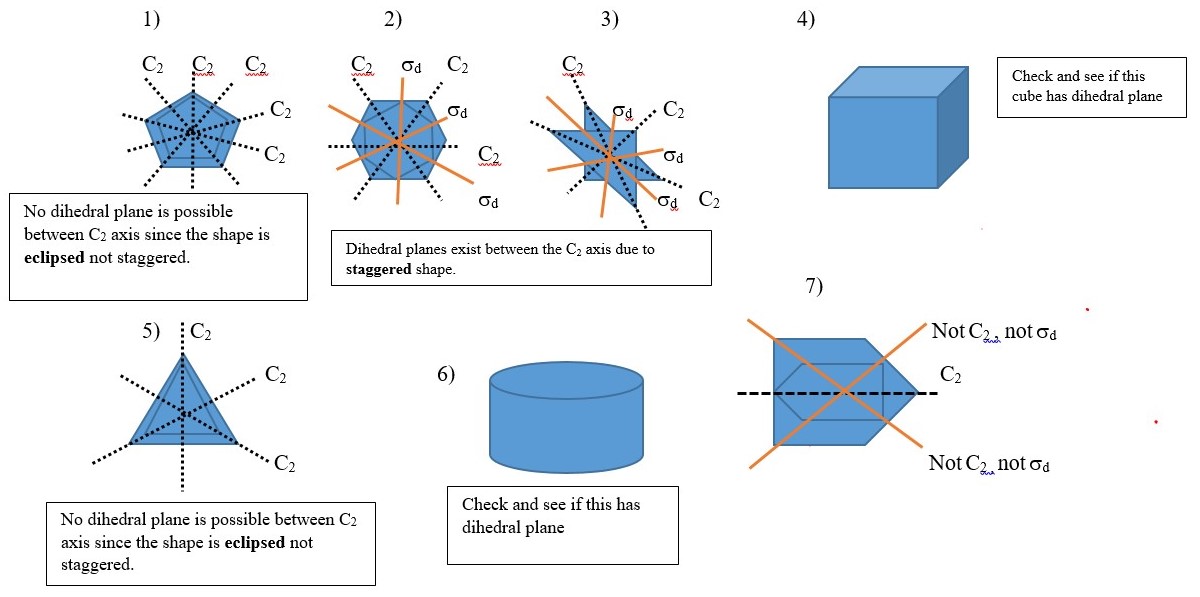
Dihedral plane (d) or σd
This is a vertical plane that bisect two C2 axis but only passes through principal Cn axis and no other point or atom such that the shape is divided into two equal parts. Examples given below have vertical planes along the C2 axes. Other examples involve objects with shape or structure made up of two layers in staggered conformations. Best view of this is obtained by using a model kit.
Multiplication of Symmetry elements
Symmetry Operations: Effect of symmetry elements on others
This is what is obtained by turning a model or shape of an object through an axis or a plane of reflection followed by another symmetry operation. For example, turning a C1 symmetry element through 360 degrees (C1) gives you an E symmetry, that is C1 x C1 = E.
Symmetry element with even number of axes raised to exponent power equal to the number of axes gives the identity element. Example C22=E, or also E= C44
Symmetry element with odd number of axes raised to exponent power equal to double number of axes gives the identity element E. Example, C36=E .
In the example below, the object has a C2 axis and two perpendicular vertical planes of symmetry ( σv and σh ) .
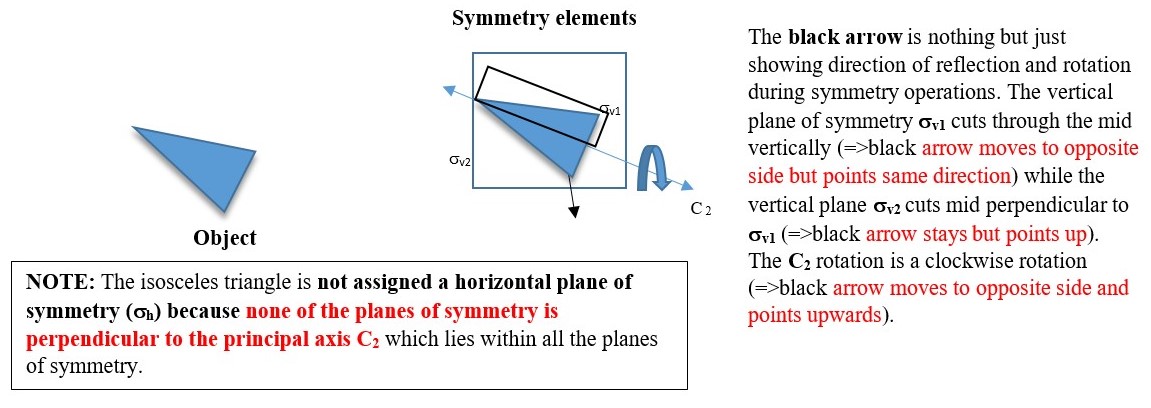
Reflection through the vertical plane (σv1) and then rotation through C2 axis is the same as reflecting the original object directly through the vertical plane σv2. This is written as C2 x σv = σv2
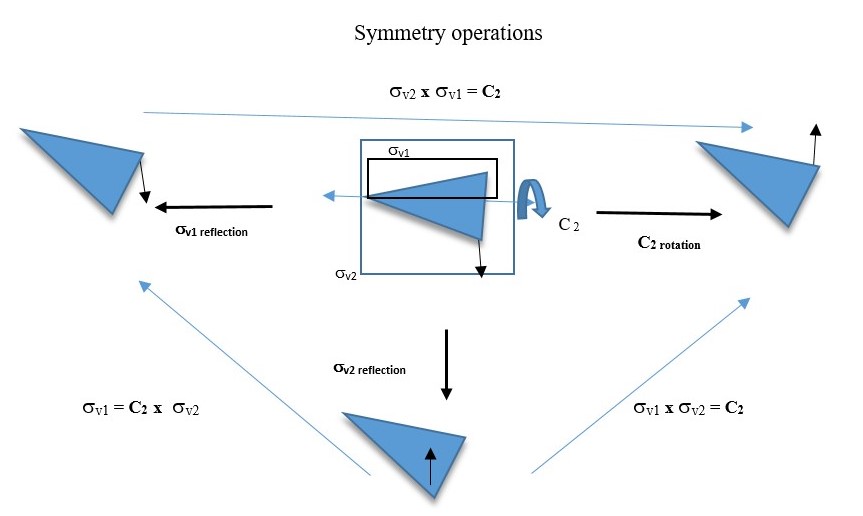
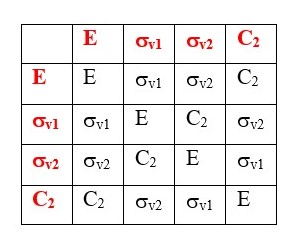
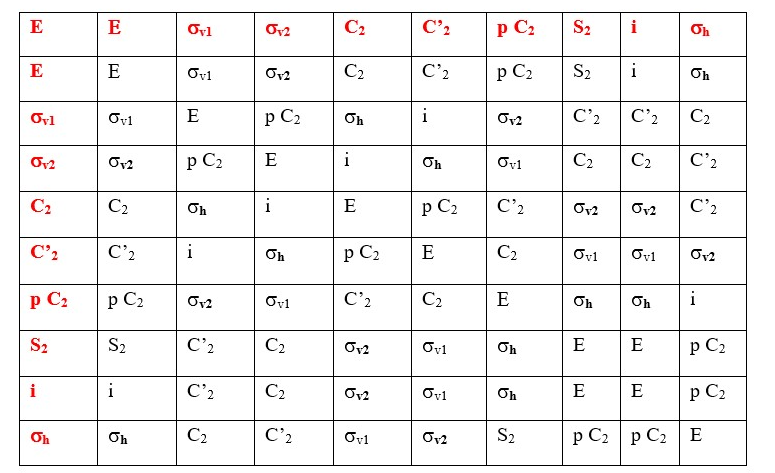
TABLE OF SYMMETRY OPERATIONS
You will also see that σv2 x σv1 = C2 This means reflecting the shape through the vertical plane (σv1) and then reflecting again through the perpendicular vertical plane (σv2) gives the same result as a C2 symmetry element.
Practice with the shape or structure of WATER (H2O) molecule.
P.S. In water structure the principal axis C2 lies with the planes of symmetry σv1 and σv2 and is not perpendicular to any of the planes so there is no horizontal plane of symmetry.
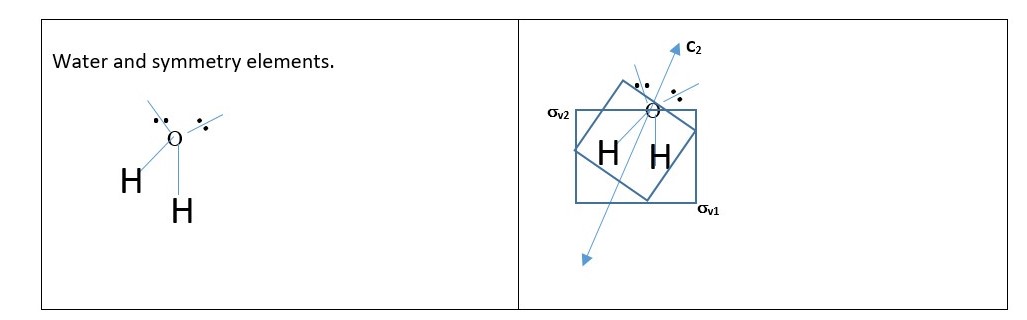
Other molecules that fit this description include SO2 , or three membered ring compounds containing one different heteroatom but two atoms of the same kind. [epoxides]
Try and practice with an equilateral triangle and write a table of the results of the symmetry operations.

Examples of compounds that fit this description include cyclopropane. The example below shows the results of rotation of a rectangle through a C2 axis followed by reflection in a vertical plane σv . This gives several results. The black arrow is nothing but just showing the orientation of the object after rotation or reflection.
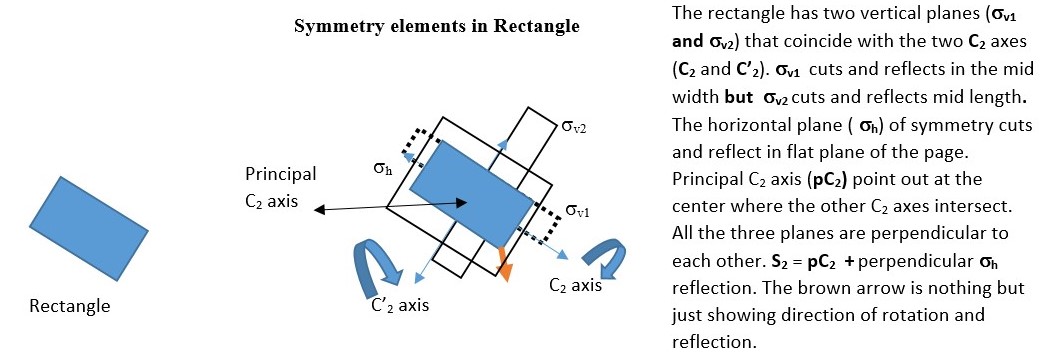
We can use this to make multiple symmetry operations and use the results to write equations. However, the equations are only true for this particular object or structure under consideration. It may not be true for another object.
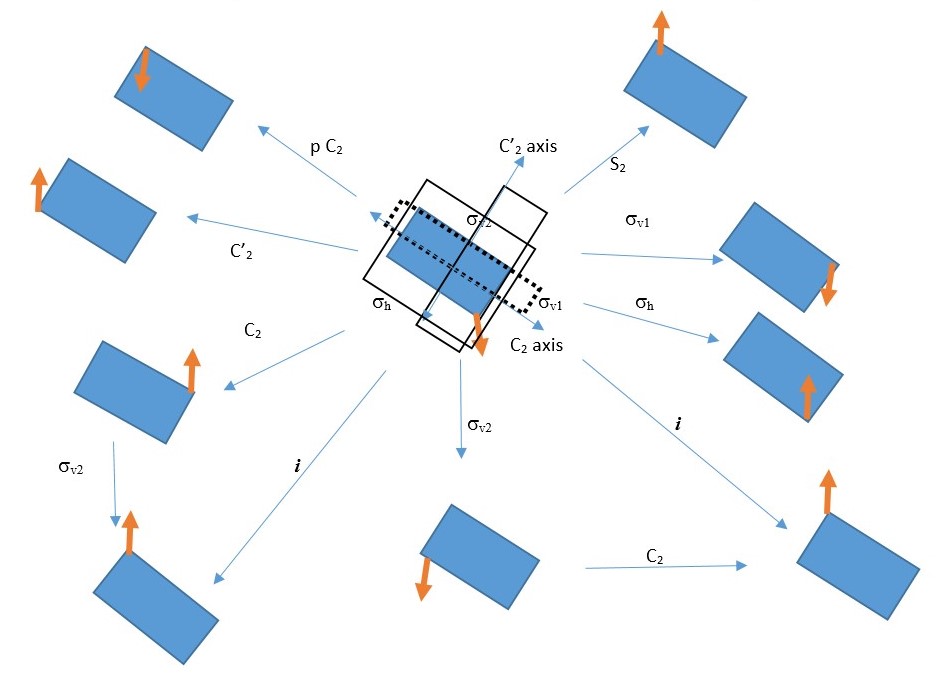
We can write several equations based on the combination of symmetry operations on the rectangle shown above. A few examples can be written as follows.
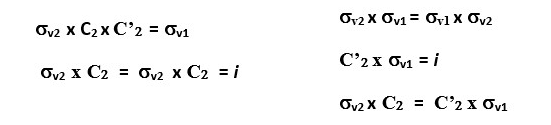
TABLE OF SYMMETRY OPERATIONS
Example of compound that fits this description is 1,3-cyclobutadiene.
Symmetry Commutations
Two symmetry operations commutes if the inverse is equal to the same result. For example, C2 x σv2 commute if σv2 x C2 gives the same result. Looking at the results in the diagram above and the equations, we can see that the two symmetry elements C2 and σv2 actually commute because the reverse operation on the rectangle gives the same result. The two symmetry elements are perpendicular to each other in the rectangle. What is the name of this symmetry element that is generated as a result of this operation. [IMPROPER ROTATION Sn] in this case it will be S2. However, in this particular case, other symmetry elements such as inversion (i) or combination of pC2 and σh will also give the same result. [S2 and i gives same results in the table above. This shows that they are the same].
POINT GROUPS
These are sets of alphanumeric characters used to designate the state of the shape or structure of an object in two-dimensional view. There are rules needed to correctly classify the point group of the shape of a structure. Examples compounds and their point groups include Water is C2v, Ammonia is C3v, HF is Cαv, HCCH, Cαh, Cyclopropane D3h etc.
The names can be seen as a Capital upper case alphabet followed by a subscript number and or an alphabet. There are many of these, but the most common first upper-case letter is usually a D or C.
D is used if there are two or more subsidiary a C2 axis that crosses a perpendicular principal axis. Example is an equilateral triangle or Cyclopropane structure. It has three C2 axis that crosses at a perpendicular C3 principal axis; therefore, we have a D3.
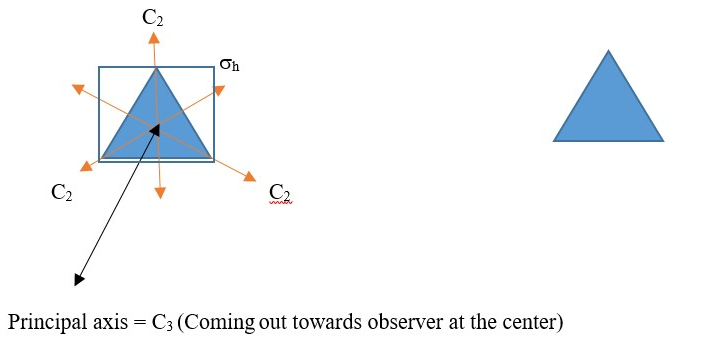
The horizontal plane of symmetry supersedes the vertical plane, so we use h instead of v. Therefore, the point group is D3h
The same results will be obtained for BCl3, B(OH)3, H3O+ and other compounds of that shape.
What is the point group of a rectangle, an isosceles triangle and a scalene triangle?
Other examples of point groups are given below using water and ammonia.

All the vertical planes are perpendicular to each other, however all of them contain or are colinear with the Principal Cn axis and not perpendicular to principal Cn axis so there is no horizontal plane of symmetry in water and ammonia.
Special Cases
HIGH SYMMETRY:
Certain objects have special names notations for the rotational axis because of very high symmetry number of rotational axis.
Examples of these point groups are listed below;
Tetrahedral shapes (Td),
Octahedral (Oh)
Dodecahedral or Icosahedral (Ih).
Infinite rotational axis:
Other objects have infinite number of rotational axis (Cα) e.g. a circle or a cylinder or a line or a dot.

Cα is perpendicular to a C2 => Dα
All the four objects have infinite number of C2 axes and perpendicular principal axis Cα
There are infinite number of vertical planes of symmetry (σv) along the Cα axis.
The plane of symmetry (σh) that cuts the cylinder into two parts is perpendicular to the Cα axis => horizontal plane (h). This is in the plane of the page for the circle or dot. Therefore, Point group = Dαh
Molecules with straight line or cylindrical shapes that fits this model are symmetrical linear molecules. e.g., HCCH, N2, F2, Cl2, CO2 etc.
However, a slight variation gives a different point group in this example below.
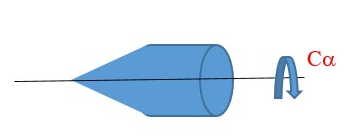
In this example, the Cα has no perpendicular C2 axis => we only have Cα principal axis.
There is infinite number of vertical planes of symmetry (σv).
There is no horizontal plane of symmetry perpendicular Cα axis => we have ONLY VERTICAL planes of symmetry (σv) lying along the Cα axis. Therefore, Point group = Cαv
Examples of molecules that fit this model are non-symmetrical linear molecules, including HCl, HBr, CO etc.
LOW SYMMETRY:
Some objects have zero or very low number of symmetry elements.
Objects with only Cn rotational axis (n=1 or more) but no plane of symmetry =>Point group= Cn
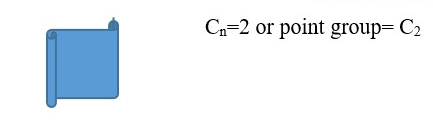
Object with Cn =1 or E rotational axis but only One plane of symmetry =>Point group= Cs
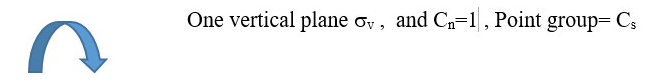
Object with Cn=1 or E and Only (i) center of inversion =>Point group = Ci
Object with Cn=1 or E and Only Sn =>Point group= Sn or S2n is related to Ci or i since S2 the same as Ci

Sn can have several values based on the value of n or principal Cn axis if there is no plane of symmetry.
Example an object with principal axis of C2 (with no plane of symmetry) and two points of inversion exchange will have S2 point group. If the object that is C1 is passed through a C2 operation and then reflected to get the same object and orientation, then the point group is S2. If the object gives the same shape and orientation after the Cn operation and there is no plane of symmetry, then the point group is Cn or Dn (if perpendicular C2 crosses the principal Cn Axis).
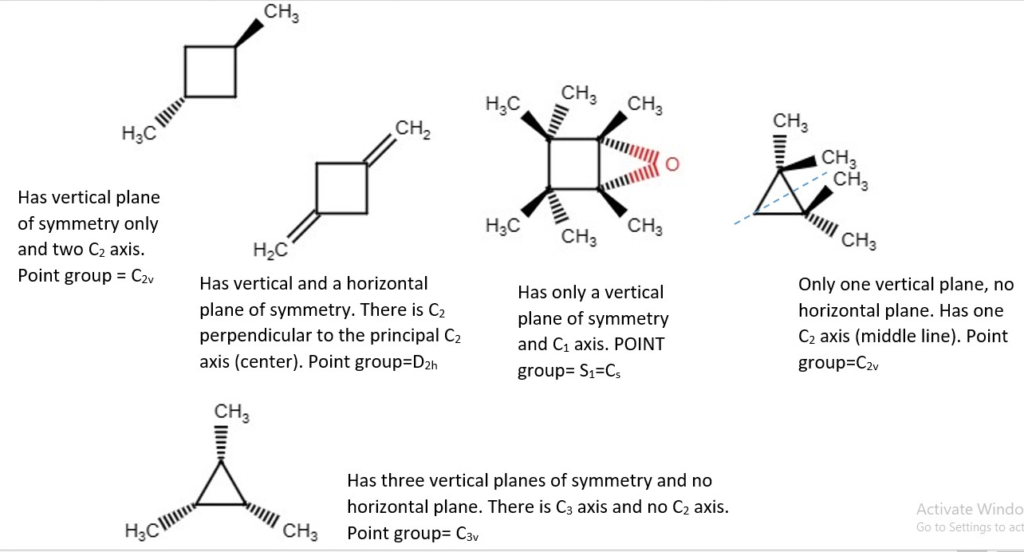
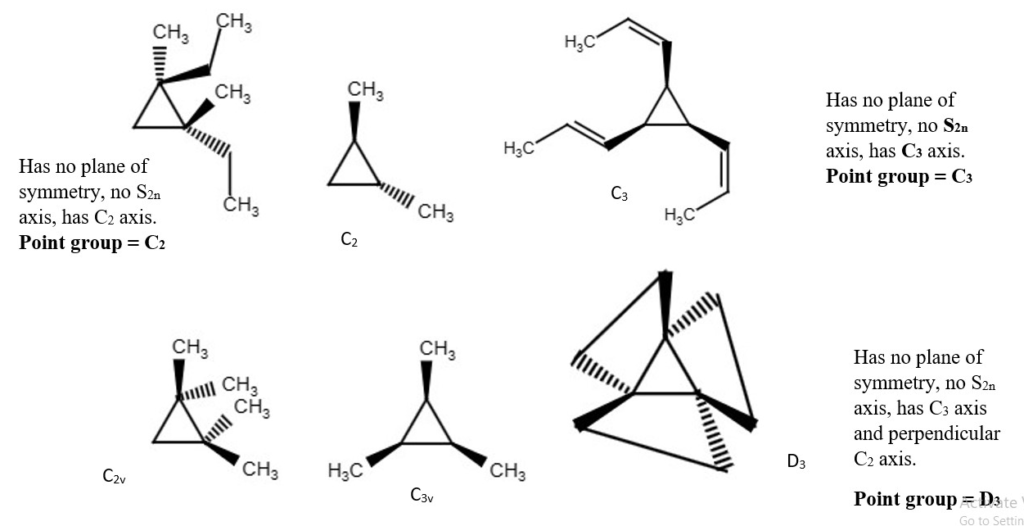
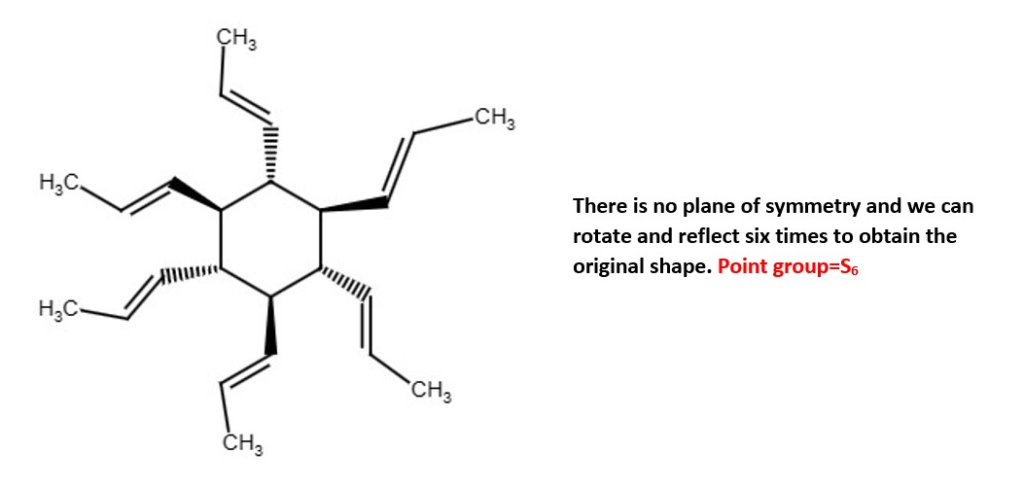
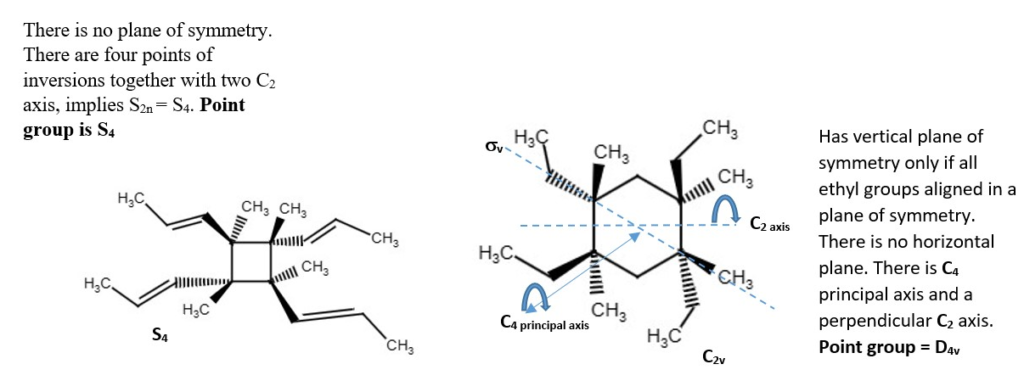
Examples of chemical structures with their symmetry and point groups are listed below.
Try and identify which compound is chiral or achiral.
;
OTHER EXAMPLES WITH LOW SYMMETRY
More difficult examples.
Other examples;
Other structures and their point groups;
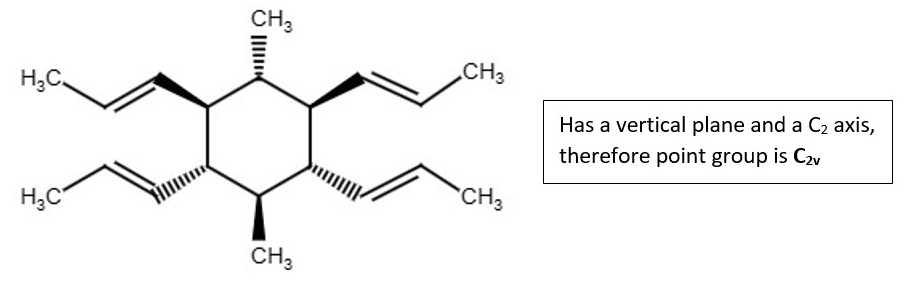
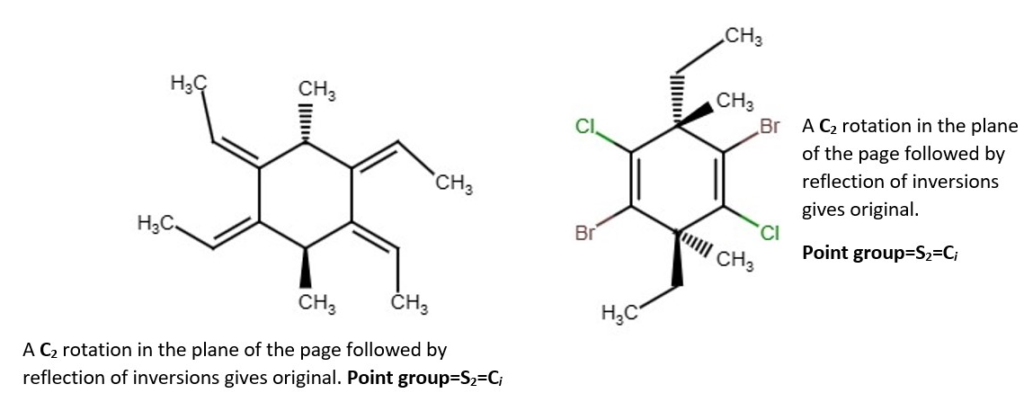
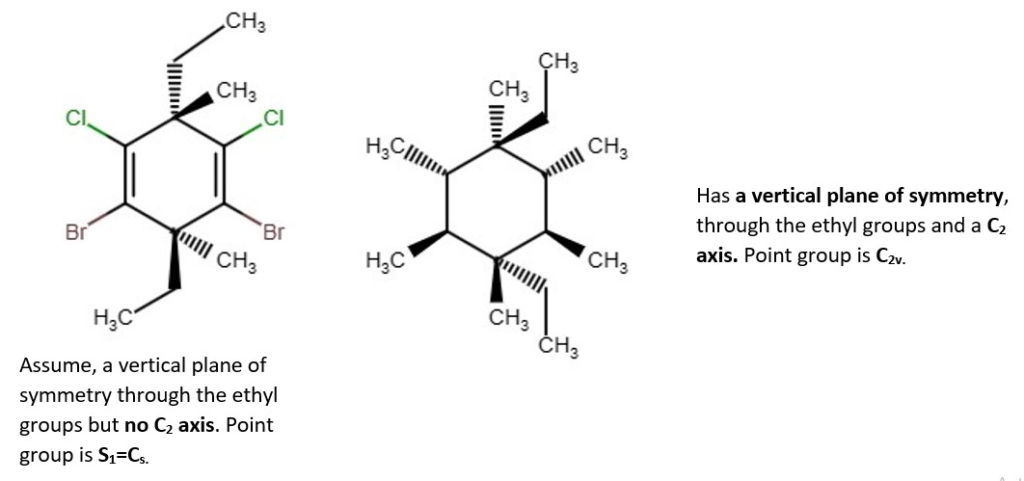

More low symmetry compounds.

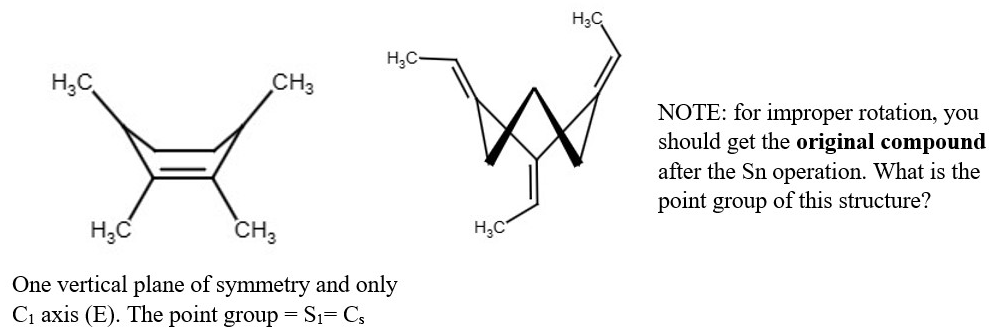
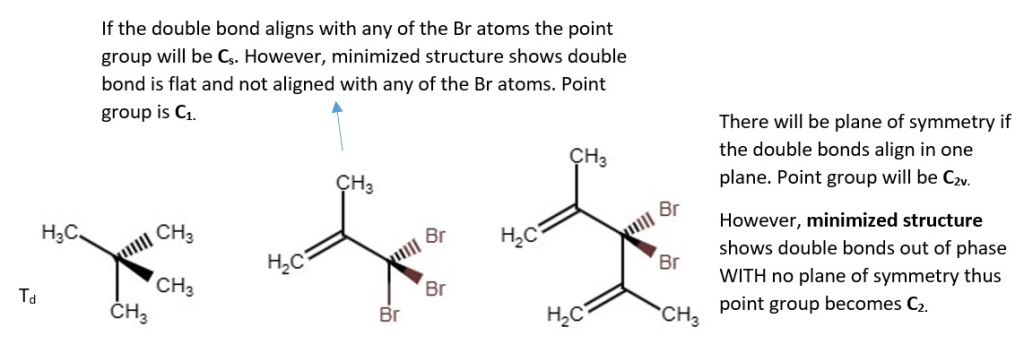
Structural derivatives of Methane and their point groups.

S3 Cyclopropane derivative:
This structure below has no plane of symmetry by careful examination. It can be rotated and reflected six times but the point group vertex corner as one rotation reflection(S2n). since each vertex point has both rotation reflection substituents. Therefore, there each count as one Sn where n=3. Point group is S3. All the structures are the same, but they are just drawn in three different ways.

Organometallic complexes (hypothetical):
These compounds shown below have no vertical plane of symmetry. however, the eclipsed conformation has horizontal plane of symmetry since the substituents are the same and aligned above and below. Point group is C3h. The other compound has no horizontal plane of symmetry since it does not have the same number of substituents above and below.
.

Organometallic complexes below are in staggered conformations. They have no vertical or horizontal plane of symmetry. There is a principal C3 axis at the center of each triangular structure. There is also a C2 axis through both structures above and below perpendicular to the C3 axis. The point group is D6.